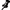prijava: |
registracija: |
aktivne teme: |
najčitanije: |
nove poruke: |
autori: |
pretraga

Nova poruka

Određeni integral (trig. podintegralna fja)

poruka: 3: |
čitano: 760: |
moderatori: DrNasty, pirat, XXX-Man, vincimus

1

+/- sve poruke
ravni prikaz
starije poruke gore

17 godina

neaktivan

offline

sri 9.4.2014 23:25

Odgovori Citiraj

Određeni integral (trig. podintegralna fja)

Pripremam se za kolokvij iz Matematike II i imam problema s jednim zadatkom ako mi možete pomoći Radi se o zadatku dolje..napravim supstituciju, rastavim na dva integrala, ali neznam što bih s ovim drugim više..mozda da krenem rjesavasti univerzalnom trigonometrijskom supstitucijom? ili kako :S.Uglavnom, hvala!

trajni link

0 0

17 godina

neaktivan

offline

čet 10.4.2014 0:28

Odgovori Citiraj

Određeni integral (trig. podintegralna fja)

Ako može pomoći, moj frend daje instrukcije iz matematike i fizike, za sve fakseve.

Moj PC

trajni link

0 0

12 godina

neaktivan

offline

uto 22.4.2014 19:57

Odgovori Citiraj

Re: Određeni integral (trig. podintegralna fja)

hm... za takve stvari postoji Bronštejn... ne znam jel ga smijete imati na ispitu, ali uglavnom ako je X=at^2+bt+c, onda je rješenje tog tvog integrala:

t/a-(b*lnX)/(2*a^2)+[(b^2-2a*c)/(2a^2)]*integral(dt/X)... e sad... taj integral dx/X ima dva moguća rješenja, koja ovise o tome dali je delta=4a*c-b^2 veće ili manje od 0.

kod tebe je delta<0, pa je rješenje u konačnici

t/a-(b*lnX)/(2*a^2)+[(b^2-2a*c)/(2a^2)]*{ln[(2a*t+b-korjen(-delta))/(2a*t+b+korjen(-delta))]}/korjen(-delta)

Poruka je uređivana zadnji put uto 22.4.2014 19:57 (ts989).

trajni link nadporuka

0 0

1

Nova poruka

00:29 Netflix u Hrvatskoj poskupljuje i do 30%
00:26 Posljednji film koji ste gledali - preporuka?
00:02 Opća rasprava o procesorima (CPU)
23:58 Revolucionarna teorija o gradnji piramida: arhitek
23:37 Eto i prvog zakona koji brani brak između ljudi i
23:31 Battlefield 6
23:22 Potvrđeno: što su djeca više uz ekrane, to su im o
23:22 EA Sports FC 26
23:21 Odgođeno glasanje o Chat controlu, još ima nade za
23:18 Koji televizor kupiti - vodič za odabir
22:07 Periferija - ultimativna tema
22:03 Ultimativna tema za odabir prijenosnika
22:03 Mercedes-Benz testira megavatno punjenje baterija,
21:59 Gledate li TV Dnevnike?
21:15 PayPal - pitanja i odgovori
20:59 Stiže AV2 kodek: bolja kvaliteta videa uz 30% manj
20:36 Rasprava o grafičkim karticama
20:26 Samsung Odyssey G7 G75F ima VA panel dijagonale od
19:44 Volvo gasi proizvodnju modela V90, posljednji prim
19:33 Rasprava o 3D printanju
19:12 Windows 11 - problemi
18:52 Smart Home Indoors – Bugovo besplatno digitalno li
18:40 Sklapanje PC konfiguracija - iznad 1300 EUR
18:39 Povodom okrugle obljetnice, Croteam je objavio vel
18:15 Kasko sa franšizom ili bez?
18:14 Kava je ukusno i zdravo piće – ako je dobro pržena
18:04 Xbox Series X
17:29 Koji monitor kupiti
16:17 Biciklizam, bicikli, oprema, staze...
16:07 Kako koristiti Revolut - digitalni pametni mobilni
16:06 Nizozemska vlada izvanrednim potezom preuzela kont
15:51 OneDrive dobiva veliku nadogradnju i AI pomoćnika
15:43 AMD i Sony prikazali su tehnološki napredak koji ć
15:14 Telemach optika
15:06 A1 kućni internet - optika
14:02 Sprej za nos protiv COVID-19 infekcije?
13:50 T-Com - prijevremeni raskid ugovora
13:03 AMD Ryzen procesori (opća tema)
12:20 Hrabrost ili ludost? Motociklist pretjecao kamion
12:12 Trebam neki program za prženje dvd-a i cd-a
11:49 Heroes of Might And Magic Olden Era
11:23 Sada se praktički sve zna o Honorovom Magicu 8 Pro
11:18 Investiranje u domene: Najneshvaćenija imovina Int
10:15 Nintendo Switch 2
09:35 Mazda 6e - 'japanska' limuzina na struju
09:28 Popusti, akcije i dobre ponude[Hardver]
09:26 Ovoga tjedna kraj je za nuklearne elektrane u Njem
09:15 Hoćemo li ikada saznati zašto je Nokia propala (ka
08:51 Sony PlayStation 5
08:22 Koji model mirovine izabrati prije odlaska u mirov
06:45 Usisavači. O da, USISIVAČI :)
06:11 Kada i kako nastaje - svijest?
01:44 Zašto se ne sjećamo svojih prvih godina
13.10. Popusti, akcije i dobre ponude[Hardver] - P&O
13.10. Pomoć pri odabiru mobitela
13.10. Dobra i loša iskustva iz BOL Forum oglasnika
13.10. Sklapanje PC konfiguracija - od 1000 do 1300 EUR
13.10. Windows 10 - problemi
13.10. Ruppu - omogućava stvaranje podsjetnika u panelu z
13.10. Xiaomi 15 Ultra
13.10. PROBLEM 9800x3d
13.10. Savjetnik za odabir odgovarajuće tipkovnice
13.10. Dječji imunosni sustav: blato i prašina, psi i "st
13.10. Kupnja brzog USB stick-a
13.10. Najgori Bond filmovi: 8 misija koje bi 007 najradi
13.10. AMD i OpenAI potpisali strateško partnerstvo za ra
13.10. Proizvođač spywarea Pegasus prelazi iz izraelskog
13.10. Pozivnice za privatne torrent trackere
13.10. Keto-dijeta: spas za liniju ili tempirana bomba za
13.10. Dota 2
13.10. Sora "pomela" ChatGPT s milijun preuzimanja u manj

vrh stranice

Copyright © 2008 - 2025 Bug d.o.o. sva prava pridržana.